XY-Chain

Description

An XY-Chain is created by following a chain of cells with exactly two candidates. Going from one cell to the next in the chain requires that the 2 connected cells must share a group and a candidate. The chain ends when the last cell shares a candidate with the first cell AND is in the same group as the first cell OR or their peers share at least 6 cells.

Reasoning

If the start and end of the chain are in the same group and share a candidate, then one of the 2 cells must take the value of that candidate. Therefore the intersection of their peers cannot hold that candidate, and therefore can be removed.

Examples

Row Example

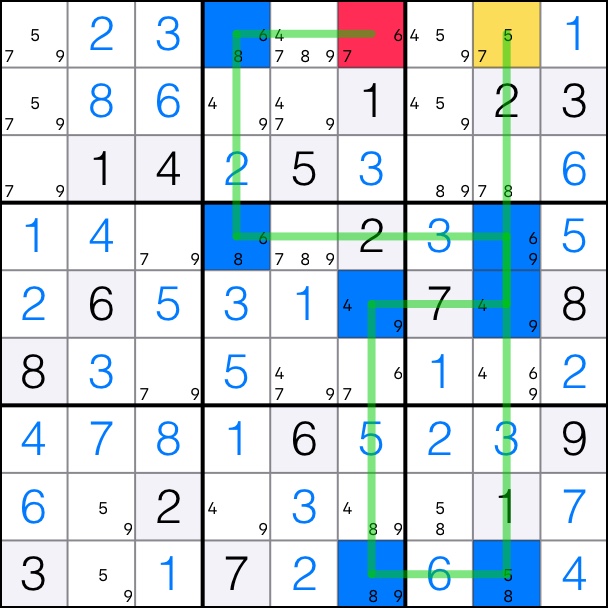
XY-Chain for digit 7 with start and end cells in row 1.

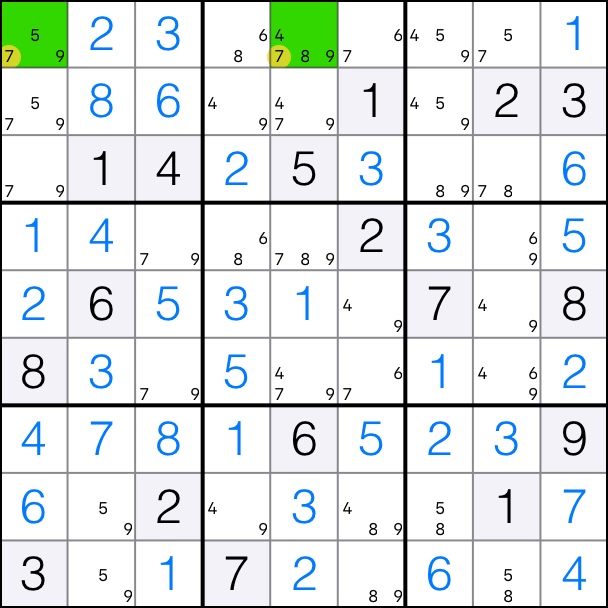
That means that candidates 7 can be removed from row 1 if they are not in the chain.

Column Example

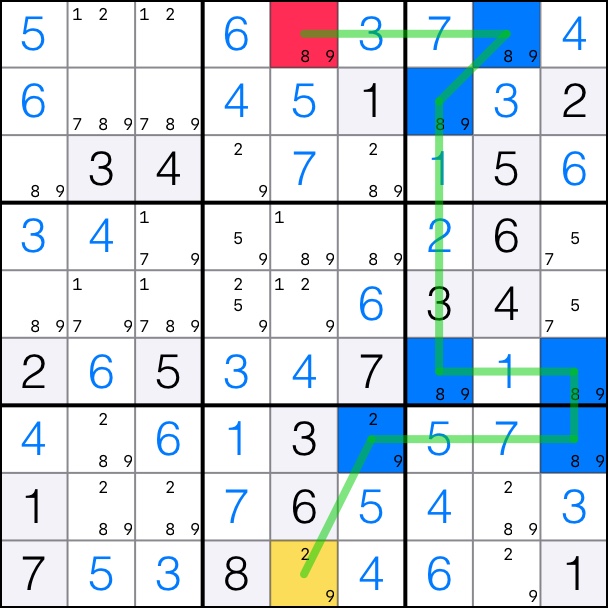
XY-Chain for digit 9 with start and end cell in column 5.

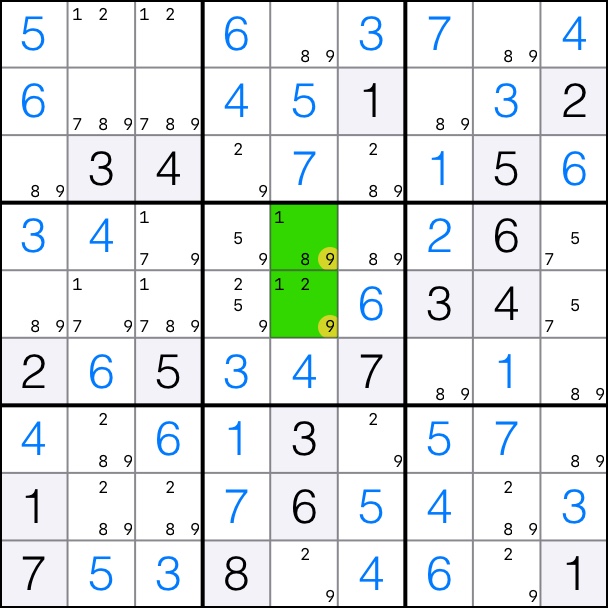
That means that candidates 9 can be removed from column 5 if they are not in the chain.

Box Example

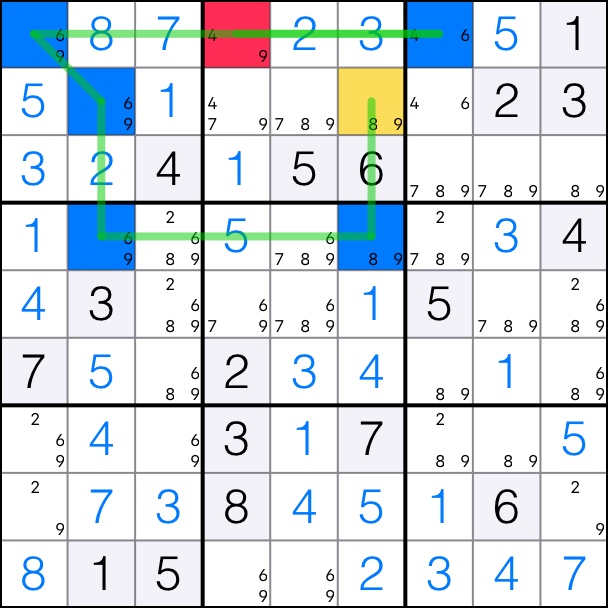
XY-Chain for digit 9 with start and end cells in box 2.

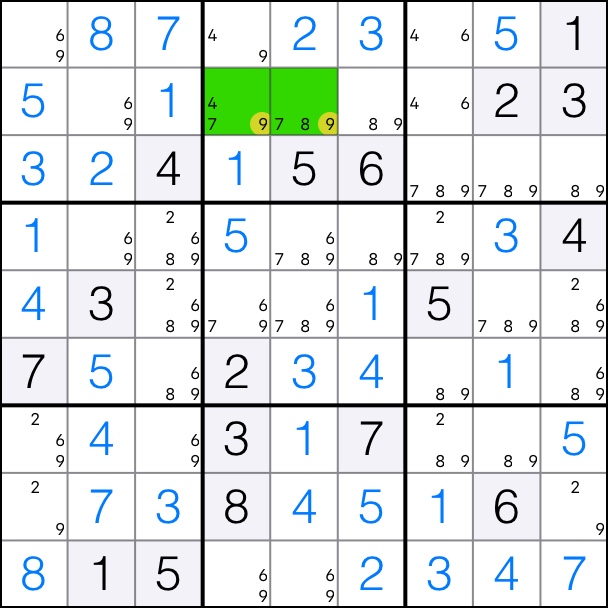
That means that candidates 9 can be removed from box 2 if they are not in the chain.

Peers Example

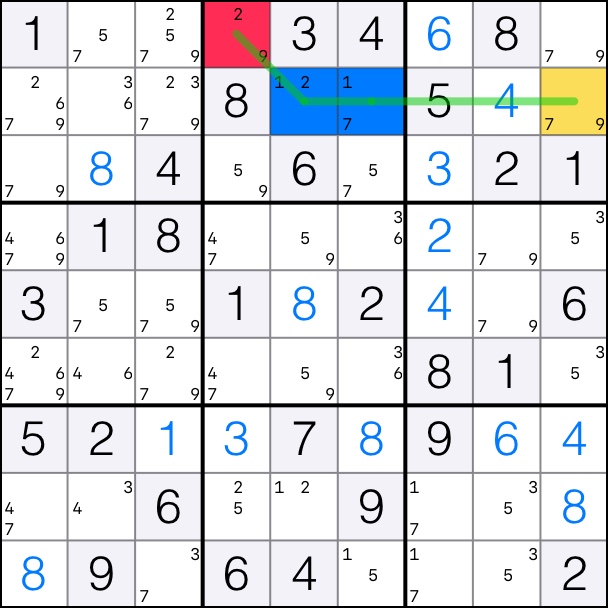
XY-Chain for digit 9 with start and end cells having at least 6 overlapping peers.

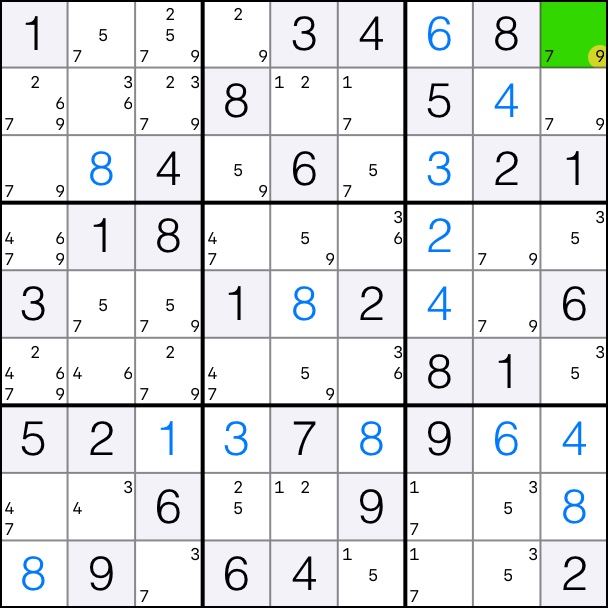
That means that candidates 9 can be removed from the intersection of the peers of the start and end cells, cell [1,9].

Algorithm

This algorithm is currently not easy to do without paper and pencil. You can take a picture of the puzzle and print it, then follow the instructions below.

  1. Fill in all the pencil marks in the puzzle.
  2. Find all the cells which have only 2 candidates.
    1. Pick a cell and see if there is another 2 candidate cell in its peers which shares a candidate.
    2. If you find one, join the cells and now look for a new cell which is in the peers of the new cell and shares the unused candidate.
    3. Keep going like this until you find a cell to end the chain. There are two ways to do that, but in both cases the first and last cell must share the candidate from the first cell which was not used yet.
      1. If the last cell is part of the peers of the first cell.
      2. If the last cell's peers intersected with the first cell's peers has at least 6 cells.
    4. Once you find a complete chain, you can remove the shared candidate between the first and last cells from the cells which form the intersection of the peers of the first and last cells.

Practice Puzzles

If you tap on the following links on an iOS device which has the Sudoku Tutor app installed, it will launch the app and open the practice puzzle. Tap hint once the puzzle is open to see the strategy in action.

Sample Puzzle 1
Sample Puzzle 2
Sample Puzzle 3
Sample Puzzle 4

Next Step

Back to Sudoku Solvers or continue to next algorithm X-Cycles