XY-Wing

Description

The XY-Wing is composed of 3 interconnected cells. The achor cell is connected to both of the other cells by sharing a different group with each of them.

  • The cells must have exactly 2 candidates each.
  • Each cell must share 1 candidate with both of the other cells.
  • The non-achor/wing cells must not share a group.
  • There must be just 3 candidates in total in the 3 cells.

Reasoning

Because the cells are connected both by sharing a group with the achor cell and 1 candidate with each other, it means that the candidate in common between the 2 wing cells MUST be in one of these cells.

That implies that the cells which are in the intersection of the peers of the 2 wing cells, cannot have their shared candidate as a possible value.

Examples

Three Box Example

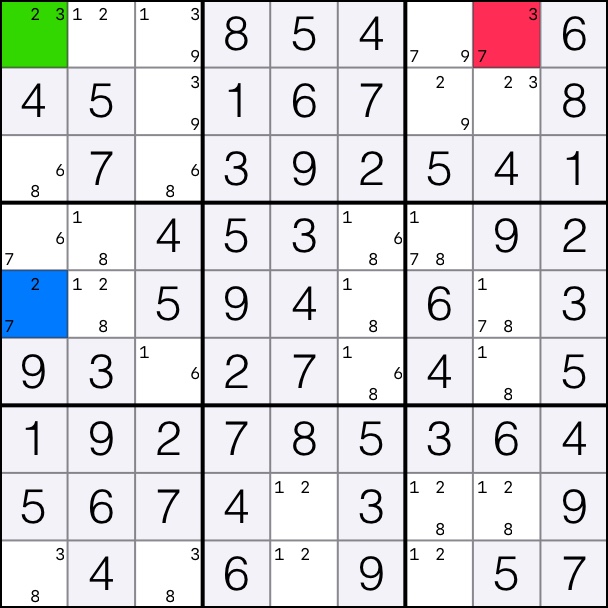
7 forms an XY-Wing in rows 1 and 5.

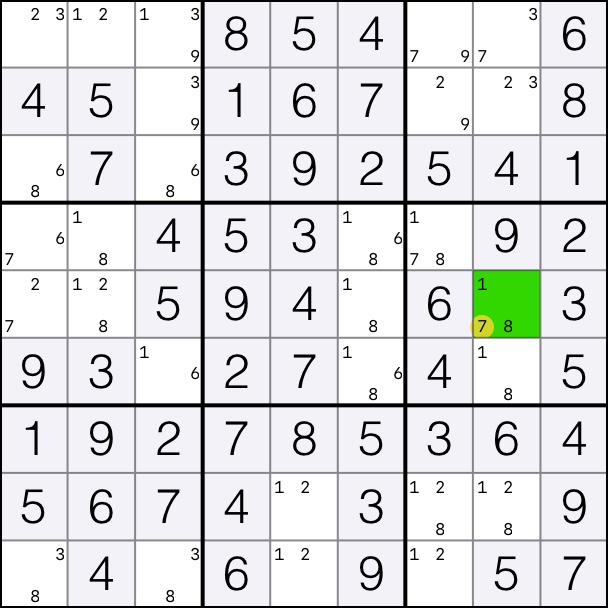
That means that candidates 7 can be removed from cell [5,8].

Row Example

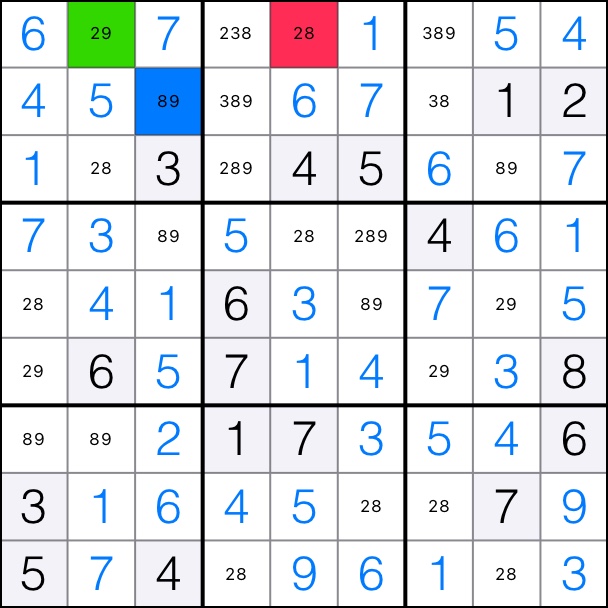
8 forms an XY-Wing in rows 1 and 2.

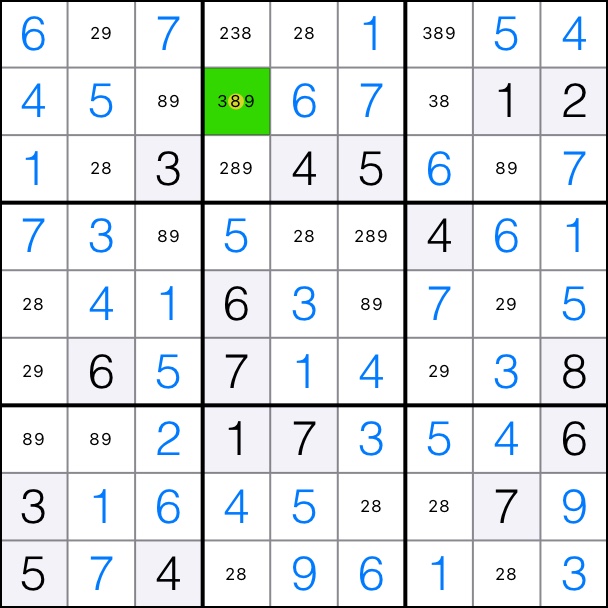
That means that candidates 8 can be removed from cell [3,4].

Column Example

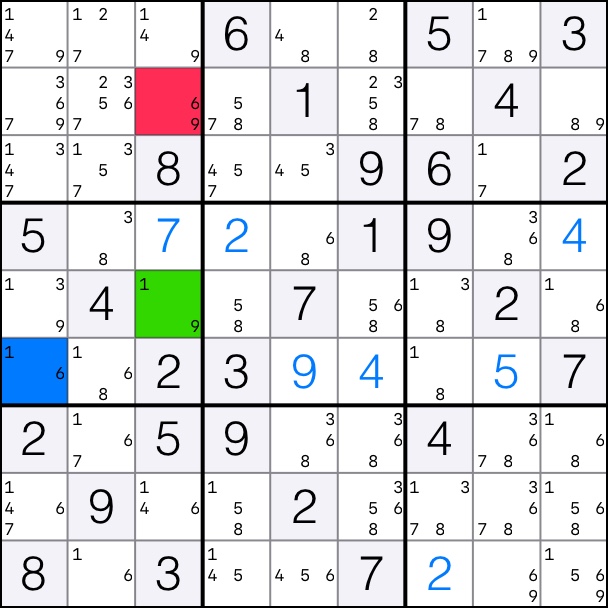
6 forms an XY-Wing on columns 1 and 3.

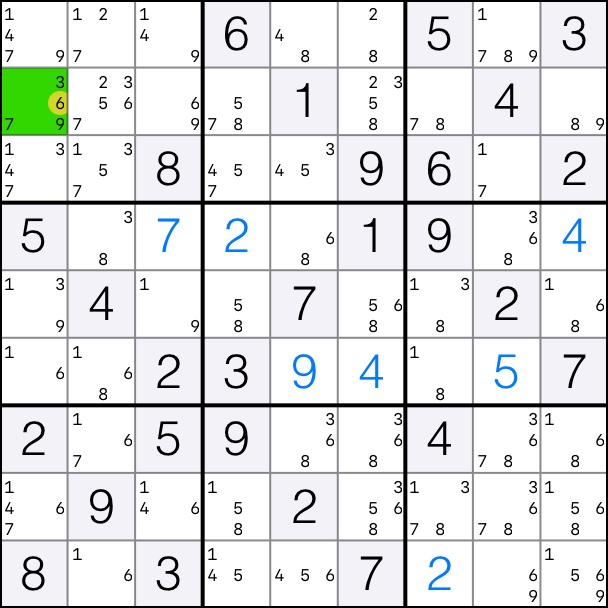
That means that candidates 6 can be removed from cell [2,1].

Algorithm

  1. Fill in all the pencil marks in the puzzle.
  2. Find all the cells which have only 2 candidates.
  3. For every combination of 3 cells with only 2 candidates
    1. Check if the 3 cells combined use only 3 unique candidates.
    2. Check if the anchor cell is connected to both other cells by a group.
    3. Check that the wing cells are NOT connected by a group.
    4. Find the digit candidate that is in common for the non-anchor cells.
    5. Find the intersecting cells of the peers of the non-anchor cells.
    6. See if that digit is present in any of the intersecting cells and remove it.

Practice Puzzles

If you tap on the following links on an iOS device which has the Sudoku Tutor app installed, it will launch the app and open the practice puzzle. Tap hint once the puzzle is open to see the strategy in action.

Sample Puzzle 1
Sample Puzzle 2
Sample Puzzle 3

Next Step

Back to Sudoku Solvers or continue to next algorithm XYZ-Wing